Quantencomputing in der Praxis mit Amazon Braket

Quantencomputer versprechen, durch die Nutzung der Gesetze der Quantenmechanik bestimmte Berechnungen deutlich schneller ausführen zu können als alle klassischen Maschinen. Heute ist Quantencomputing keine Zukunftsmusik mehr – verschiedene Firmen bauen seit ein paar Jahren Quantenprozessoren auf Basis verschiedener Technologien und Anwendungsentwickler:innen und Wissenschaftler:innen aus Industrie und Forschung suchen nach ersten industrierelevanten Anwendungen. Dank Cloud-Computing ist die Technologie auch für die breite Öffentlichkeit zugänglich.
Die bekannteste Formalisierung dessen, was wir unter einem modernen Computer verstehen, lieferte Turing 1936 mit der später als "Turing-Maschine" bekannten Idee [1]. Diese Maschine schreibt und liest Symbole auf ein unendliches Band und entscheidet basierend auf seinem Zustand den jeweils nächsten Schritt. In heutigen Computern sind die Symbole und Zustände aus Bits und Gates, elektronischen Bauteilen, die die Bits manipulieren und miteinander verknüpfen, zusammengesetzt.
In der ersten Hälfte des 20. Jahrhunderts entdeckten Physiker:innen, dass die Welt im Kleinen anderen Gesetzen folgt als die bis dahin bekannte klassische Mechanik. Die mathematischen Gesetze der Quantenmechanik lassen scheinbar paradoxe Situationen zu: Teilchen können an mehreren Orten zugleich sein (Superposition) oder die Polarisation eines Photons überträgt sich durch Messung scheinbar instantan an einen anderen Ort (Nicht-Lokalität, Teleportation). Bald stellte sich die Frage, was passiert, wenn man die Mathematik und Physik der Quantenmechanik auf die Bits des klassischen Computers anwendet. Das klassische Bit wird dann zum "Qubit", der kleinsten Informationseinheit eines Quantencomputers. Durch Ausnutzen quantenmechanischer Eigenschaften soll dieser in der Lage sein, bestimmte Rechenprobleme schneller zu lösen als klassische Turing-Maschinen – so die Hoffnung.
Was ist Quantencomputing?
Vom Bit zum Qubit
Ein Schalter, also ein System, welches nur in den zwei Zuständen "an" und "aus" beobachtet werden kann, ist in der Quantenmechanik ein Qubit. Da die Quantenmechanik die Natur nach unserem besten Wissen beschreibt, sollten also alle Transistoren in heutigen Prozessoren bereits Realisierungen von Qubits sein. Ihre Quanteneigenschaften werden allerdings von unvermeidbaren Umgebungseinflüssen verdeckt: Temperatur, elektromagnetischer Strahlung, Interaktion mit Teilchen der Luft und der umgebenden Elektronik. Diese Einflüsse führen dazu, dass die Qubits nach außen betrachtet ihre quantenmechanischen Eigenschaften verlieren und sich wie klassische Bits verhalten, also keine Qubits mehr sind. Einen Teil dieses Prozesses bezeichnet man mit dem Begriff "Dekohärenz".
Möchte man einen Quantencomputer bauen, kommt es also darauf an, die Qubits möglichst gut von diesen Störeinflüssen zu isolieren. Dies ist der Gegenstand aktueller weltweiter ingenieurwissenschaftlicher Anstrengungen. Zusätzlich sind Verfahren zur Fehlerkorrektur notwendig, dazu später mehr.
Die Mathematik hinter Qubits
Ein klassisches Bit kann nur die Werte 0 oder 1 annehmen. Ein Qubit dagegen beschreibt man durch einen zweidimensionalen komplexen Vektor der Länge 1. Wie in der Schulmathematik ist so ein Vektor also zunächst ein Pfeil in einem 2D-Koordinatensystem, allerdings bedeutet "komplex" hierbei, dass die Koeffizienten komplexe Zahlen sind, also einen Real- und einen Imaginärteil haben.
Die möglichen Zustände so eines komplexen zweidimensionalen Einheitsvektors werden oft mit Hilfe der sogenannten Bloch-Kugel dargestellt (Abb. 1). Diese sieht aus wie ein Globus, dessen Nordpol mit dem Einheitsvektor entlang einer der Achsen des Vektorraumes (bezeichnet mit dem Symbol |0>) und der Südpol mit dem Einheitsvektor entlang der anderen Achse (|1>) identifiziert wird. Alle anderen möglichen Zustände eines Qubits korrespondieren jeweils mit anderen Punkten auf der Oberfläche dieser Kugel.
Das Auslesen eines Qubits (physikalisch spricht man hier von einer "Messung") hat im Bild der Bloch-Kugel jeweils zur Folge, dass der Zustand des Qubits augenblicklich auf den Nord- oder Südpol springt oder "kollabiert". Dabei korrespondiert die ursprüngliche Nähe des Zustandes zu einem dieser Pole jeweils mit der Wahrscheinlichkeit des Kollapses auf eben diesen Pol.
Quanten-Speedup
Die Idee, quantenmechanische Systeme als Computer zu nutzen, geht auf den Physiker Richard Feynman zurück [2]. Er erkannte, dass bestimmte in der Natur vorkommende quantenmechanische System zu komplex sind, um sie mit klassischer Rechenhardware zu simulieren. Stattdessen könnte man ein künstliches quantenmechanisches System im Labor aufbauen, über dessen Komponenten man bessere Kontrolle hat und welches sich dem ersten System ähnlich verhält. Diese Art, ein Quantensystem durch ein weiteres Quantensystem zu simulieren, stellt einen "analogen" Quantencomputer dar.
In den Neunzigerjahren fand der Mathematiker Peter Shor zum ersten Mal einen Algorithmus, der stattdessen auf einem universellen digitalen Quantencomputer (also einem System mit Qubits und diskreten Logik-Operationen) laufen kann und der eine exponentiell bessere Skalierung für das Problem der Zerlegung von Zahlen in ihre Primfaktoren aufweist [3]. Da das Problem der Primfaktorzerlegung relevant für viele heute gängige Verschlüsselungsalgorithmen ist, ist dieser Quantenalgorithmus weiterhin Gegenstand der Forschung. Die Welt muss sich auf eine Zeit vorbereiten, in der Quantencomputer so weit ausgereift sind, dass sie einige verbreitete Verschlüsselungsalgorithmen brechen können.
Shor's Algorithmus und weitere skalieren nicht deshalb besser mit der Problemgröße als ihre klassischen Gegenstücke, weil Qubits etwa "mehrere Werte gleichzeitig" berechnen könnten. Spezialisierte Probleme, die sich auf Quantencomputern effektiv ausführen lassen, machen sich in der Regel bestimmte mathematische Strukturen zunutze. Im Fall von Shor's Algorithmus ist dies die Tatsache, dass sich das Problem auf das Finden der Periode einer Funktion reduzieren lässt. Qubits lassen sich mathematisch in gewisser Weise durch Pfeile auf einer Kugeloberfläche beschreiben (s. Die Mathematik hinter Qubits). Kugeloberflächen haben eine "periodische" Eigenschaft: Läuft man auf der Oberfläche immer weiter geradeaus, kommt man irgendwann wieder am Ausgangspunkt an. Shor's Algorithmus nutzt diese Eigenschaft zusammen mit der Möglichkeit quantenmechanischer Interferenz geschickt aus.
Das Finden solcher Algorithmen mit garantierten "Quanten-Speedups" gleicht der Suche nach einer Nadel im Heuhaufen. Bisher sind nur wenige solcher Algorithmen bekannt. Manchmal ist auch das Problem, das sie lösen, nicht von besonderem praktischem Nutzen, wie in Google's Experiment von 2019, in der sie ihrem Computer "Quantum Supremacy" bescheinigen [4]. Ein Teil der heutigen Forschung und viele der Anwendungen konzentrieren sich daher auf heuristische Verfahren, die ein effektiv besseres Skalierungsverhalten mit der Problemgröße zeigen.
Aktueller Stand von Quantencomputing
Fehlerkorrektur
Heute existierende Quantencomputer bringen lediglich eine Handvoll Qubits mit, die zudem nur eine begrenzte Anzahl von Logikoperationen erlauben, bevor das System dekoheriert. Durch den unvermeidbaren Einfluss der Umgebung kollabieren sie kurze Zeit nach ihrer Präparation zu klassischen Zuständen. Um diese Effekte zu umgehen, sind in den letzten Jahren mehrere theoretische Verfahren zur Fehlerkorrektur auf Quantencomputern entstanden. Die meisten dieser Verfahren basieren auf dem Prinzip von "logischen Qubits": Mehrere nahe beieinander liegende Qubits werden zu größeren Einheiten verknüpft, die sich dann nach außen wie perfekte oder zumindest bessere Qubits verhalten. Der dadurch notwendige Overhead von physischen Qubits wird auch von der Fehlerrate der verwendeten Qubit-Technologie bestimmt. Sowohl Google als auch Amazon haben vor kurzem die erfolgreiche Herstellung von fehlerkorrigierten Qubits bekanntgegeben [5;6]. Trotzdem sind Gate-basierte Quantenalgorithmen mit garantierten Speedups, wie etwa Shor's Algorithmus, für heutige Systeme und relevante Problemgrößen noch nicht praktikabel. Aufgrund dessen versucht man sich in der Anwendung oft auf bestimmte Probleme zu konzentrieren, für die die Imperfektion der Qubits weniger relevant ist, oder man nutzt verschiedene Tricks, um die Dekohärenz besser zu kontrollieren.
Die aktuelle Phase in der Entwicklung des Quantencomputing hat den Namen der "NISQ"-Ära erhalten [7]. NISQ steht hierbei für "Noisy Intermediate-Scale Quantum", also etwa "Quantencomputer mittlerer Größenordnung mit fehlerbehafteten Qubits". In der Wissenschaft und Industrie wird daran gearbeitet, in dieser NISQ-Ära bereits Anwendungsfälle zu finden, die einen Mehrwert für relevante Probleme bieten. Oft wird dieser Mehrwert als "Quantum Advantage" bezeichnet.
Quantenalgorithmen
Eine vielversprechende Familie von Algorithmen für die NISQ-Ära sind die sogenannten hybriden Quantenalgorithmen. Bei diesen werden klassische Instruktionen mit einem Quanten-Teil kombiniert. Hierbei handelt es sich meist um verschiedene heuristische Näherungsverfahren. Ein Beispiel ist der "Quantum Approximate Optimization Algorithm" (QAOA), bei dem das Problem in eine mathematische Beschreibung für ein parametrisiertes quantenmechanisches System übersetzt wird [8]. Dieses System kann dann über die Gates eines Quantencomputers “simuliert” werden. Dabei kommen verschiedene Parameter zum Einsatz, die nach jedem Durchlauf variieren und durch einen klassischen Algorithmus optimiert werden. QAOA ist zum Beispiel zur Behandlung des Industrie-relevanten "Job-Shop-Scheduling-Problems" vorgeschlagen worden, welches sich mit der Frage beschäftigt, wie eine Anzahl von Aufgaben am effizientesten auf eine Menge von bearbeitenden Maschinen verteilt werden kann [9]. Ob QAOA allerdings im Vergleich zu rein klassischen Algorithmen grundsätzlich Vorteile bringt, ist noch nicht abschließend geklärt.
Auf der Suche nach Quantum Advantage in der NISQ-Ära ist auch das sogenannte "adiabatische Quantencomputing" ein vielversprechendes Verfahren. Wie bei QAOA wird auch hier die Lösung eines Problems zunächst in die Beschreibung eines Quantensystems übersetzt. Die Qubits werden dann initial in einem Lösungszustand eines anderen, einfacheren Systems präpariert. Das System wird jetzt langsam (adiabatisch) vom "einfachen" System in das gewünschte, das Problem darstellende, "komplexe" System überführt. Man kann mathematisch zeigen, dass der Zustand der Qubits, einmal präpariert im Zustand niedrigster Energie des einfachen Systems, sich dann in den Zustand niedrigster Energie des komplexen Systems und damit in die bestmögliche Lösung überführen lässt. Adiabatisches Quantencomputing ermöglicht zudem einen interessanten Trick bei der Suche eines Problems mit Quantum Advantage: Welche Quantensysteme mit klassischen Rechnern einfach zu simulieren sind, ist mittlerweile hinreichend untersucht und bekannt. Betrachtet man also solche, für welche die klassischen Simulationen bisher nicht machbar sind, hat man beste Chancen, klassische Algorithmen in den Schatten zu stellen.
Eng verwandt ist das "Quantum Annealing" (QA), welches insbesondere durch die kanadische Firma D-Wave Aufmerksamkeit erhalten hat [10]. Die auf QA spezialisierten Quantencomputer von D-Wave haben bereits heute eine deutlich höhere Anzahl von kontrollierbaren Qubits als andere Systeme, können allerdings nur spezielle Optimierungsprobleme mittels QA lösen.

Hardware
Aktuell werden für die existierenden Plattformen verschiedene Technologien zur Realisierung von Qubits verwendet. Bei den sogenannten Flux-Qubits werden kleine supraleitende Ringe verwendet, durch die ein mikroskopischer Strom fließt und die durch Barrieren, den Josephson Junctions, unterbrochen werden [11]. Solche supraleitende Qubits kommen z. B. in den Chips von Google (s. Abb.), IBM, D-Wave, Rigetti und IQM zum Einsatz [12;13]. Alternative Qubits bestehen aus in Laserfallen gefangenen ionisierten Atomen (IonQ, Quantinuum) oder auch Rydberg-Atomen, Atomen in hochangeregten elektronischen Zuständen (QuEra, PASQAL) [14;15;16;17].
Einen grundsätzlich anderen Ansatz verfolgt das "Linear Optical Quantum Computing". Hier bestehen die Qubits aus Photonen (Lichtteilchen) in hochqualitativen Lichtleitern. Die besondere Herausforderung ist dabei, dass Photonen praktisch nicht miteinander wechselwirken und somit zunächst die für den universellen Einsatz unerlässlichen 2-Qubit-Gates nicht realisierbar scheinen. Ein vielversprechender Ausweg ist hier das Mess-basierte Quantencomputing, bei dem ein initial hoch verschränkter Quantenzustand durch Messungen einzelner Qubits immer weiter reduziert wird. Diese Idee verfolgt z. B. das Startup PsiQuantum [18].
Quantencomputing in der Praxis
Projekte in der Industrie
Quantencomputing ist längst nicht mehr nur ein akademisches Betätigungsfeld. Verschiedene Player in der Industrie arbeiten bereits an Anwendungen, von denen sie sich Vorteile in ihren Geschäftsfeldern erhoffen. Grob lassen sich diese in drei verschiedene Kategorien unterteilen: Optimierung (das Finden von Lösungen für kombinatorische Probleme), Simulation (Materialforschung und Chemie, aber auch Finanzmärkte) sowie Quantum AI (Nutzung von Quantencomputing beim Training von KI-Modellen). Wir fokussieren uns im Folgenden auf den Bereich der Optimierung.
Optimierungsprobleme kann man allgemein mit der Suche nach lokalen Minima (oder Maxima) in einem großen, in der Regel nicht extensiv erforschbaren Lösungsraum beschreiben. Weist dieser Lösungsraum nur wenige lokale Minima auf, sind klassische Optimierungsalgorithmen hier in der Regel sehr effizient. Ist dies aber nicht gegeben, kann die klassische Exploration des Lösungsraums in solchen lokalen Extrempunkten stecken bleiben – der Algorithmus findet dann lokal brauchbare Lösungen, hat aber keine Möglichkeiten, in die Nähe einer besseren globalen Lösung zu gelangen. Hier erhofft man sich eine bessere Performance von Quantenalgorithmen, die auf QAOA oder adiabatischem Quantencomputing basieren. Viele solcher Probleme sind relevant für die Industrie, weshalb viele große Unternehmen dazu eigene Forschung betreiben.
Beispielsweise betrachtet ein deutscher Automobilkonzern das sogenannte "Paint-Shop-Problem", um zu beantworten, in welcher Reihenfolge Autoteile ihre Lackierung erhalten sollen, um den Prozess zu optimieren und nutzt dabei die D-Wave-Plattform [19]. Auch in der Logistikbranche gibt es enormes Potential bei der Optimierung von Fahrzeugrouten, sodass hier z. B. ein multinationales Energieunternehmen zusammen mit IBM an Quantenalgorithmen arbeitet [20]. Ebenso erhofft sich die Flugzeugindustrie einen Quanten-Boost bei der Bewältigung ihrer Herausforderungen, so veröffentlichte etwa Airbus zusammen mit IonQ einen Ansatz zur Optimierung von Frachtverladung [21].
Quantencomputing könnte auch bei der Lösung von großen gesellschaftlichen Herausforderungen relevant werden – dies ist die Idee hinter der "Quantum Climate Challenge", die seit einiger Zeit jährlich von der Unternehmensberatung Deloitte veranstaltet wird [22]. Teilnehmer:innen widmen sich hier in Teams explorativ der Lösung von bei der Bewältigung der Klimakrise relevanten Problemen. Beispielsweise ging es in der Iteration 2024 um die Vorhersage von Flutkatastrophen mit Quantum Machine Learning. In der Vergangenheit wurden auch die Kategorien Simulation (Entwicklung von Algorithmen zum Finden geeigneter Materialien für Carbon Capture & Storage (CCS)) und Optimierung (Reduktion von Trajektorien im Flugverkehr) in der Quantum Climate Challenge behandelt. Der Wettbewerb richtet sich längst nicht mehr nur an Teams aus dem universitären Umfeld, sondern es sollen explizit Personen mit einem Background in klassischem Computing angesprochen werden, um ihnen einen Einstieg in die Welt des Quantencomputing zu ermöglichen.
Quantencomputing in der Cloud
Es gibt nur wenige Firmen auf der Welt, die Quantencomputer bauen können – würde man sich ein Exemplar selbst zulegen wollen, wäre man schnell einige Millionen Dollar los und hat seinen Keller hoffentlich bereits zum Labor ausgebaut. Stattdessen haben sich in den letzten Jahren mehrere Anbieter etabliert, die Rechenzeit auf ihren Quantencomputern über das Internet verkaufen. Marktführer ist hier IBM, das mit der Quantum Platform Zugang zu seinen auf supraleitenden Qubits basierenden Prozessoren anbietet [23]. IBM ist auch Hauptentwickler der Open-Source-Bibliothek "qiskit", die einen Entwurf von Quanten-Schaltkreisen und deren Ausführung aus Python heraus ermöglicht [24]. Aber auch viele weitere Hersteller bieten mittlerweile Cloud-Services für die eigene Hardware an.
Zusätzlich gibt es Firmen, die Rechenzeit auf diversen Quanten-Backends weiterverkaufen und in der Cloud anbieten. Ein Beispiel ist hier AWS mit der Braket-Plattform, es gibt aber auch z. B. das deutsche Startup Kipu Quantum mit der Plattform PlanQK [25]. Der Vorteil ist hier, dass man sich nicht an eine bestimmte Architektur bindet und neue Hardware nutzen kann, sobald sie in die Plattform integriert wird. Ein Vorteil der großen Hyperscaler ist jedoch, dass diese Systeme dann auch in den diversen weiteren in der Cloud vorfindbaren Services integriert sind.
Amazon Braket
Seit 2020 stellt AWS mit dem Service Amazon Braket einen Fully-Managed Cloud-Service zum Entwickeln und Testen von Quantencomputing-Lösungen zur Verfügung [26]. Der Service kann genutzt werden, um Algorithmen zu entwickeln und durch eine Vielzahl von vorgefertigten Workloads den Einstieg in das Thema Quantencomputing zu finden. Die einzige Voraussetzung hierfür ist ein bestehender AWS-Account.
Brakets
Die Bra-Ket-Schreibweise (auch als Dirac Notation bekannt) ist eine der Standardnotationen der Quantenmechanik. Sie wurde 1939 vom englischen Physik-Nobelpreisträger Paul Dirac eingeführt, um quantenmechanische Zustände einfach zu beschreiben. Im Wesentlichen besteht sie aus sogenannten "Angle Brackets" | x > und < y |, die von Dirac als "ket" und "bra" bezeichnet wurden. Mathematisch beschreiben diese Objekte Vektoren in einem abstrakten Vektorraum bzw. dessen Abbildungen (s. auch Die Mathematik hinter Qubits) [27]. Aufgrund der herausragenden Bedeutung von Diracs Arbeit hat AWS seinen Quantum-Computing-Service nach der Braket-Schreibweise benannt.
Funktionsweise
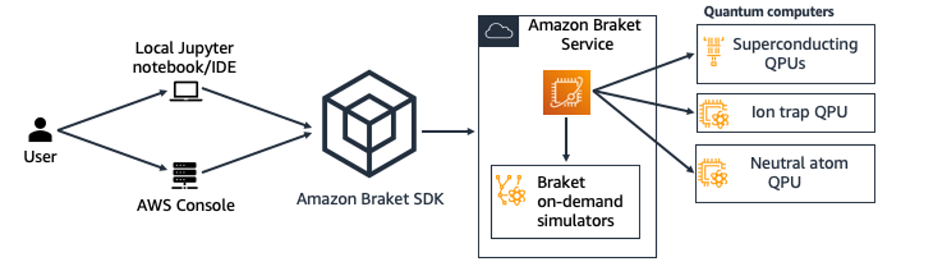
Amazon Braket wird über ein Open Source Software Development Kit (SDK) angesteuert und kann damit in bestehende Python-Workflows und Entwicklungsumgebungen wie lokale Jupyter-Notebooks integriert werden [28]. Darüber hinaus stehen in der AWS-Konsole auch Beispiel-Notebooks mit einer Vielzahl an vorgefertigten Algorithmen zur Verfügung.
Quantencomputing-Programme können aktuell auf den bereitgestellten Quantencomputern von IonQ, IQM, QuEra und Rigetti ausgeführt werden (s. Architekturdiagramm) [29]. Dabei sollte jedoch stets abgewogen werden, ob der aktuelle Stand der eigenen Entwicklung Tests auf realer Quanten-Hardware notwendig macht, da dies zu erheblichen finanziellen Aufwänden führen kann. Wissenschaftler:innen können allerdings auf das AWS Cloud Credit for Research Progam von AWS zurückgreifen, um Kosten einzusparen [30].
Eine gute Alternative für die Entwicklung von Prototypen und das Testen von Algorithmen stellen die mitgelieferten Simulatoren in Amazon Braket dar. Hier gibt es zwei Alternativen: Der lokale Simulator kann auf dem eigenen PC/Notebook ausgeführt werden, um erste Designs zu testen. Hiermit können, bei entsprechender Rechenpower, bis zu 25 Qubits (ohne Noise, also dem bei realen Geräten unvermeidbaren Umgebungsrauschen) oder 12 Qubits (mit Noise) simuliert werden, ohne dass zusätzliche Kosten entstehen. Für weiterführende Entwicklungen/Tests stellt AWS außerdem verschiedene On-Demand-Simulatoren zur Verfügung. Dabei können Kapazitäten von bis zu 50 Qubits (abhängig vom genutzten Simulator) verwendet werden. Da es sich hierbei um Rechenleistung in der AWS-Cloud handelt, fallen pro Minute der Nutzung Kosten an.
In jedem Fall können zusätzlich zu den von Braket bereitgestellten Compute-Ressourcen alle anderen AWS-Services wie Identity and Access Management (IAM) etc. verwendet werden, um komplexere Systeme aufzubauen. Zahlreiche Open-Source-Beispiele gibt es auf GitHub [31]. Sehr nützlich insbesondere bei Verwendung echter Quanten-Hardware ist das Projekt "cost-control-for-amazon-braket", das genutzt werden kann, um anfallende Kosten für QPU-Ressourcen in (fast) Echtzeit zu tracken und optional den Zugriff beim Überschreiten vorher festgelegter Budgets zu unterbinden [32]. Somit lässt sich sicherstellen, dass der eigene Finanzplan stets eingehalten wird.
Erste Schritte
Um Amazon Braket nutzen zu können, muss zuerst ein AWS-Account erstellt werden. Der Account ist dabei zunächst kostenfrei. Vor weiteren Experimenten macht es Sinn, sich mit Grundkonzepten der AWS-Cloud wie Regionen, User-Management etc. vertraut zu machen. Insbesondere sollte man zusätzlich zum Root-User mindestens einen weiteren IAM-User erstellen, der zum Aufsetzen der Services genutzt wird.
Nach der erfolgreichen Anmeldung nutzt man die Suchfunktion der AWS-Weboberfläche, um zum Braket-Service zu navigieren. Braket steht momentan nur in ausgewählten AWS-Regionen zur Verfügung. Nach Auswahl etwa der Region "Europe (London)" gelangt man in das Braket Dashboard und nutzt anschließend den "Get Started"-Assistenten zum Einrichten des Accounts. Eine Step-by-Step-Anleitung kann in der AWS-Dokumentation gefunden werden [33].
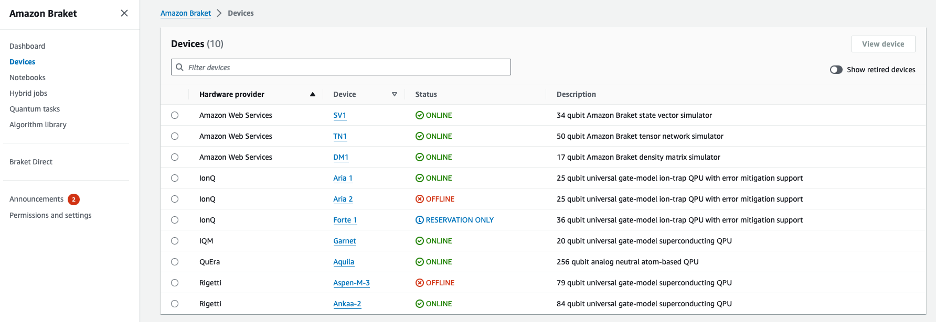
Unter dem Menüpunkt "Devices" findet man die zur Verfügung stehenden Computer-Ressourcen und Simulatoren mit Metainformationen. Unter "Notebooks" können eigene Jupyter-Notebooks erstellt und/oder Beispiel-Notebooks genutzt werden. Für die Nutzung von Notebooks innerhalb der AWS-Konsole wird eine EC2-Instanz benötigt, die zusätzliche Kosten verursacht. Solange nicht an den Notebooks gearbeitet wird, sollte die Instanz also gestoppt werden.
Statt dem Weg über die AWS-Konsole kann man auch das SDK für Python mit einem Paketmanager der Wahl oder direkt aus dem Source-Code installieren [34]. Das folgende Beispiel erstellt ein Virtual Environment in Python und installiert das SDK (+ Abhängigkeiten) via pip:
~$ python3 -m venv .braket
~$ source ./.braket/bin/activate
~$ pip install amazon-braket-sdk
Um die Installation zu überprüfen, kann
~$ pip show amazon-braket-sdkgenutzt werden. Ein erstes, sehr rudimentäres Beispiel zur Benutzung des lokalen Simulators findet man direkt im Repo des Python SDK [35]. Dabei handelt es sich um die Präparation von zwei Qubits in einem sogenannten Bell-Zustand und die darauffolgende Messung.
from braket.circuits import Circuit
from braket.devices import LocalSimulator
device = LocalSimulator()
bell = Circuit().h(0).cnot(0, 1)
print(device.run(bell, shots=100).result().measurement_counts)
Um das Skript auszuführen, kann z. B.
~$ python3 local_bell.pyverwendet werden. Nach erfolgreicher Ausführung der Simulation erhält man einen Rückgabewert der Form
Counter({ 00: 53, 11: 47 })Dies ist das Ergebnis der Ausführung des Circuits auf dem Simulator mit 100 Durchführungen ("Shots") und der Ergebnisstatistik der auf den Qubits ausgeführten Messungen. In 53 der 100 Fälle sind also beide Qubits im Zustand "0" gemessen worden, in den anderen Fällen im Zustand "1" [36].
Bell State Measurement
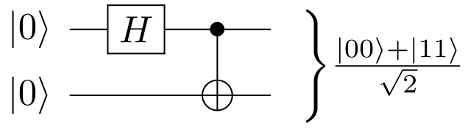
Bell States (auch EPR-States genannt) sind bestimmte quantenmechanische Zustände, bestehend aus zwei Qubits. Sie sind relevant, weil sie einen einfachen Fall von Verschränkung darstellen – eine Eigenschaft quantenmechanischer Systeme, die deren klassische Simulation erschwert und deshalb ein wichtiger Bestandteil eines Algorithmus mit Quantum Advantage sein könnte. Im Beispiel-Skript wird ein Hadamard-Gate (.h(0)) und ein CNOT-Gate (.cnot(0,1)) unserer Circuit-Instanz verwendet, um den Zustand zu präparieren. Dies lässt sich in einen einfachen quantenmechanischen Schaltplan übersetzen (s. Abb. 5).
Gelesen von links nach rechts starten wir mit zwei Qubits (hier als Ket-Zustände |0> dargestellt) als Basis, die dem Anfangszustand unseres Circuit entsprechen. Im nächsten Schritt wird das obere Qubit durch das Hadamard-Gate so manipuliert, dass eine Superposition aus Zuständen |0> und |1> entsteht, z. B. (|0> + |1>). Abhängig vom so entstandenen Zustand auf der oberen Linie invertiert das CNOT Gate den Wert des zweiten Qubits und es entsteht ein Bell-Zustand (|00> + |11>). Eine der Eigenschaften des Bell-Zustandes ist, dass sich die zwei verschiedenen Zustände mit einer 50/50-Wahrscheinlichkeit messen lassen. Unsere Testmessung mit 100 Shots (d. h. 100 Versuchen) ergab eine Verteilung von 53 Treffern für |00> und 47 Treffer für |11>, was dem theoretischen Ergebnis nahekommt. Die Tatsache der nicht exakten Verteilung lässt sich auf die statistische Natur der Messung zurückführen und wird im Quantum Computing auch als Shot Noise bezeichnet.
Alternativen
Neben AWS gibt es natürlich auch andere Anbieter für Quantencomputing und damit verbundene Services. Dabei sind einerseits die beiden weiteren Cloud-Hyperscaler Google und Microsoft zu nennen sowie der Marktführer IBM [37;38;39]. Dazu kommen zahlreiche weitere Anbieter, die verteilt über den ganzen Globus das Angebot immer weiter ausbauen.
AWS bietet hier die Besonderheit, dass das System einerseits gut mit den bestehenden Konzepten der AWS-Cloud zu verbinden ist (z. B. User-Management, Access-Rights, Storage Buckets) und andererseits ein einheitliches SDK und eine Abstraktionsschicht für die Nutzung verschiedener Quantenhardware bietet. Es muss allerdings erwähnt werden, dass State-of-the-Art-Forschung häufig auf bestimmte Geräte und sogar einzelne Qubits optimiert werden muss, was einer Abstraktionsschicht entgegensteht.
Fazit
Quantencomputing ist ein faszinierendes Feld – bereits in der heutigen NISQ-Ära arbeiten verschiedene Player aus Industrie und Forschung an relevanten Einsatzgebieten. Cloud-Computing ermöglicht es zudem jedem, die Konzepte von Quantencomputing selbst zu erforschen und auszuprobieren. Amazon Braket ist hierbei nur eine von vielen Möglichkeiten.
Danksagung
Die Autoren bedanken sich bei Dr. Sebastian Stern (AWS), Dr. Anne-Maria Visuri (Kipu Quantum) sowie Dr. Barbara Wellmann (Deloitte) für Diskussionen, viele Informationen über Quantencomputing in der Praxis sowie hilfreiche Vorschläge zu diesem Artikel.
- Turing, Alan Mathison (1936). "On computable numbers, with an application to the Entscheidungsproblem" (PDF). Proceedings of the London Mathematical Society. 58: 230–265.
- Feynman, R.P. Simulating physics with computers. Int J Theor Phys 21, 467–488 (1982).
- Shor, P. W. “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer.” SIAM Rev. 41 (1995): 303-332.
- Arute, F., Arya, K., Babbush, R. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
- Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 614, 676–681 (2023).
- H. Levine et al. (2024). Demonstrating a Long-Coherence Dual-Rail Erasure Qubit Using Tunable Transmons. Phys. Rev. X 14, 011051
- Brooks, M. (2019). Beyond quantum supremacy: the hunt for useful quantum computers. Nature. 574. 19-21.
- Farhi, E. & Goldstone, J. & Gutmann, S. (2014). A Quantum Approximate Optimization Algorithm.
- K. Kurowski, T. Pecyna, M. Slysz, R. Różycki, G. Waligóra, J. Wȩglarz, Application of quantum approximate optimization algorithm to job shop scheduling problem, European Journal of Operational Research, Volume 310, Issue 2, 2023, 518-528.
- DWave: Unlock the Power of Practical Quantum Computing Today
- Orlando, T. P.; Mooij, J. E.; Tian, Lin; Van Der Wal, Caspar H.; Levitov, L. S.; Lloyd, Seth; Mazo, J. J. (1999). "Superconducting persistent-current qubit". Physical Review B. 60 (22): 15398–15413.
- Rigetti
- IQM
- IONQ
- Quantinuum
- Quera
- Pascal
- PSIQuantum
- Volkswagen - Paint Shop Optimization with Quantum Annealing
- Harwood, S. & Gambella, C. & Trenev, D. & Simonetto, A. & Bernal Neira, D. & Greenberg, D. (2021). Formulating and Solving Routing Problems on Quantum Computers. IEEE Transactions on Quantum Engineering. PP. 1-1.
- IONQ: Learn Quantum: Cargo Loading Optimization
- Deloitte: Deloitte's Quantum Climate Challenge
- IBM Quantum
- Github: qiskit
- PlanQK
- Braket
- P. A. M. Dirac (1939). A new notation for quantum mechanics. Mathematical Proceedings of the Cambridge Philosophical Society, 35, pp 416-418
- Github: amazon-braket-sdk-python
- AWS: Amazon-Braket-Quantencomputer
- AWS: AWS Cloud Credit for Research
- AWS: AWS Samples
- AWS: Introducing a cost control solution for Amazon Braket
- AWS: Getting started with Amazon Braket
- Github: amazon-braket-sdk-python
- Github: local_bell.py
- GitHub: examples
- QuantumAI
- Microsoft: Azure Quantum Elements
- IBM Quantum