Machine Learning: Regressionen und Neuronale Netze

Kaum eine Technologie hat sich in den letzten Jahren so in unserem Alltag breit gemacht wie das maschinelle Lernen. Wenn Sie im Internet bei einer Bestellung weitere Einkaufsvorschläge erhalten oder Sie eine Pflanzenart anhand eines Bilds erkennen wollen, einen Text in eine andere Sprache übersetzen lassen oder sich den Umsatz vorhersagen lassen – für all das wird heute maschinelles Lernen eingesetzt.
Ein großer Teil dieser Fragestellungen sind Klassifikationsaufgaben, bei denen anhand von Eingangswerten eine ganze Zahl (stellvertretend für eine Klasse, z. B. 0/1 als Ja/Nein-Entscheidung) als Ergebnis erwartet wird. Ein weiterer großer Teil sind Regressionsaufgaben, bei denen ein kontinuierlicher Wert (z. B. ein Umsatz oder eine Restlebensdauer) als Ergebnis erwartet wird. Dieser Beitrag behandelt verschiedene Regressionsverfahren anhand ausgewählter Beispiele.
Vom klassischen Programm zum maschinellen Lernen
In den ersten Anfängen der Datenverarbeitung war das gängige Programmier-Modell die Abbildung von Daten auf ein Ergebnis (EVA: Eingabe - Verarbeitung - Ausgabe). Die Regeln wurden durch den Programmierer über fest verdrahtete Regeln implementiert.
Dieses Modell lässt sich erweitern, indem man die Regeln in einer Wissensbasis auslagert, wobei diese Regeln mit Regel-Editoren bearbeitet werden. In der eigentlichen Anwendung zieht ein Programm (die Problemlösungskomponente oder Inferenzmaschine) aus den Daten bzw. Benutzereingaben Schlussfolgerungen anhand der Regeln. Bei einer Änderung der Wissensbasis bleibt die Inferenzmaschine unverändert. Dieses Modell war typisch für die Expertensysteme.
Beim Maschinellen Lernen geht man noch einen Schritt weiter: Zu Beginn des Lernvorgangs legt man ein Modell – meist mit einer festen Zahl von Parametern – fest. Für dieses Modell wird der Lernvorgang an einer Stichprobe, den Lerndaten, durchgeführt. In den Parametern des Modells werden die Ergebnisse des Lernvorgangs abgelegt.
Danach erfolgt die Vorhersage (predict()) anhand des Modells und der erlernten Parameter für eine neue Stichprobe, seien es Testdaten oder Daten, für die ein Ergebnis zu bestimmen ist.
Regressionen
Null- und Voll-Modelle
Bei einer sehr großen Zahl von Lernvorgängen geht es um Regressionen, bei denen man einen kontinuierlichen Wert als Ergebnis bestimmt. Ein einfacher Fall ist die lineare Regression mit einer Variablen (univariate Regression): Man setzt eine Geradengleichung an und minimiert den quadratischen Fehler durch Variation der Steigung und des Achsenabschnitts.

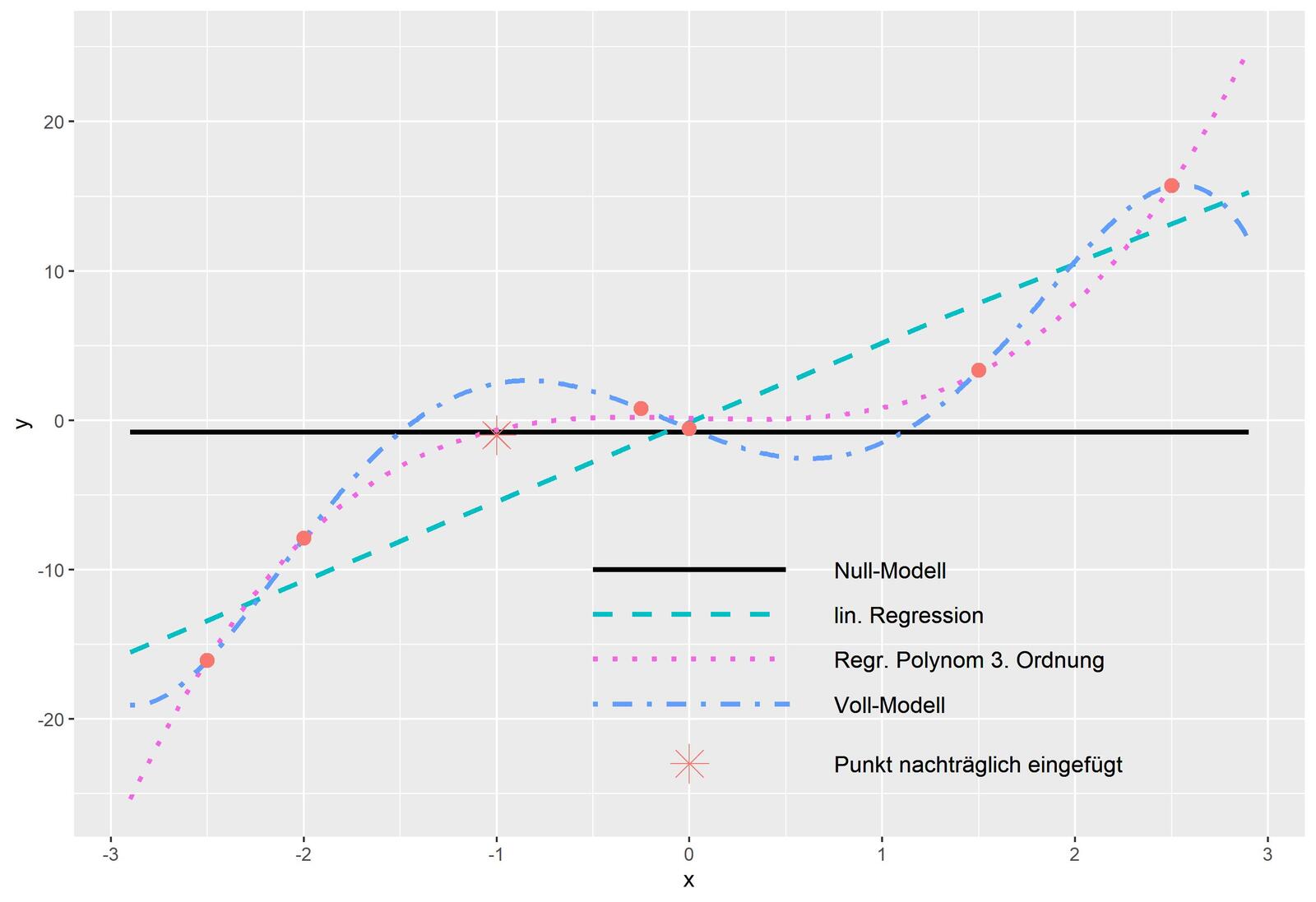
Ein noch einfacheres Modell wäre die Beschreibung der Daten durch lediglich einen Parameter, beispielsweise durch den Mittelwert. Ein solches Modell nennt man Null-Modell, dessen Leistungsfähigkeit man durch die Fehlerquadratsumme SS0 beschreiben kann. In der anderen Richtung kann man ein Modell auch auf der Basis von Polynomen aufstellen. Hat man genauso viele Parameter wie Punkte festgelegt, kann man alle Punkte ohne Fehler (z. B. mithilfe eines Newtonschen Interpolationspolynoms) beschreiben.
Auch andere Funktionen können verwendet werden, wobei deren maximale sinnvolle Anzahl von Parametern durch die Zahl der vorhandenen Punkte und ihrer Merkmale beschränkt ist. Ein solches Modell nennt man Voll-Modell. Dieses Modell mag zwar alle berücksichtigten Punkte ohne Fehler beschreiben, für nachträglich hinzugefügte Punkte liegt das Modell jedoch meist daneben. Man spricht dann von Überanpassung ("Auswendig-Lernen").
In der Praxis beginnt man mit einer kleinen Parameterzahl und erhöht sie schrittweise, bis Überanpassung einsetzt. Dieses Modell nennt man das aktuelle Modell, welches eine Fehlerquadratsumme SSa aufweist. Die allgemein übliche Größe zur Bewertung eines Regressions-Modells ist das Bestimmtheitsmaß
Für ein Null-Modell ist das Bestimmtheitsmaß R2=0 (wegen SSa=SS0), ein Voll-Modell weist den Maximalwert R2=1 (wegen SSa=0) auf.
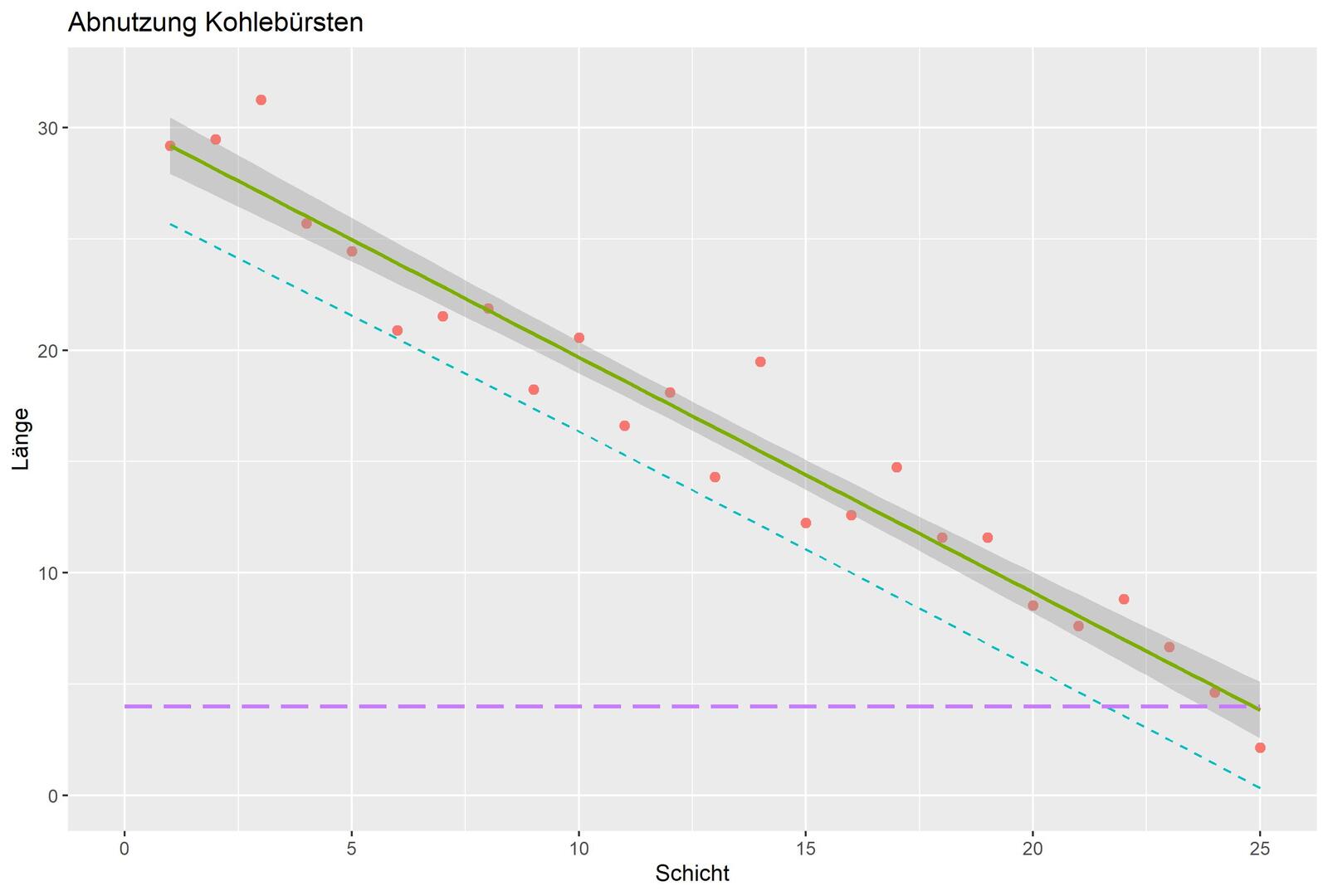
Auf der Basis statistischer Modelle (lineare oder generalisierte lineare Modelle) lassen sich Aussagen über das Verhalten der Regression machen, wie Abb. 7 veranschaulicht. Beispielsweise entspricht der eingezeichnete graue Bereich einem Vertrauensbereich von 0,95, die schräg nach unten verlaufende gestrichelte Linie entspricht einer unteren Intervallgrenze ("predict").
Um die Regressionen robust gegen Streuung in den Daten zu machen, gibt es eine Vielzahl weiterer Methoden wie z. B. Regularisierung [1], M-Schätzer [2] oder LQS-Regressionen [2].
Der Boston-Datensatz
Das Regressions-Verfahren kann auch bei mehreren Variablen angewandt werden (multivariate Regression). Der Boston-Housing-Datensatz ist ein häufig eingesetzter Beispieldatensatz als Benchmark für Regressionen [4]. Er enthält Informationen, die vom US Census Service über Wohnraum in der Gegend von Boston (Massachusetts) gesammelt wurden. Der Datensatz ist mit 506 Fällen vergleichsweise klein.
Das Merkmal "medv" (Medianwert der Preise von Eigentumswohnungen in 1.000 USD) soll in Abhängigkeit von 13 anderen Merkmalen (wie z. B. Anzahl der Zimmer oder Alter) bestimmt werden. Ein großer Teil der Variablen kann nicht als normalverteilt betrachtet werden. Beispielsweise gibt es keine Häuser oberhalb eines Kaufpreises von $50.000; bei den Entfernungen zur Autobahn ("rad") liegen 74 Prozent der Werte zwischen 0 und 8 Meilen. In 25 Prozent aller weiteren Fälle beträgt diese Entfernung dann exakt 24 Meilen, dazwischen befinden sich keine Werte. Vermutlich wurden bei dieser (und auch weiterer) Variablen andere Sachverhalte verschlüsselt. Man darf bei einer linearen Regression daher keine Wunder erwarten.
Setzt man bei dieser Regression das weit verbreitete GNU-Statistik-Paket R ein, so erhält man mit einem einfachen Aufruf das Ergebnis der Regression mit einem R2 =0,7406:
> lm_boston <- lm(medv ∼ ., data = Boston)
Variablenreduktion mit PCA
Bei der linearen Regression wird eine Ausgleichsgerade gesucht, die das Fehlerquadrat minimiert. Unter der Voraussetzung, dass die Werte (annähernd) normalverteilt sind, kann man im Fall zweier Merkmale die Werte zentrieren und so die Betrachtung auf einen Parameter reduzieren. Skaliert man jetzt noch die verschiedenen Merkmale, so dass die Varianzen σi2=1 betragen, und trägt die Punktepaare in einem Koordinatensystem auf, kann man die einzelnen Flächen bestimmen, welche die Punkte mit den Achsen aufspannen. Die Flächen dieser Rechtecke aus dem zweiten und vierten Quadranten werden von den Flächen des ersten und dritten Quadranten subtrahiert. Man erhält so den Wert der Kovarianz.
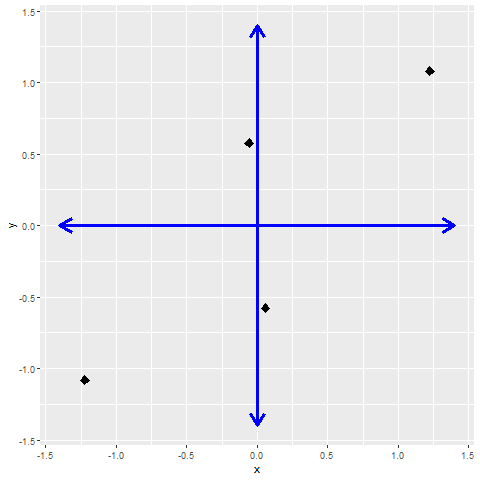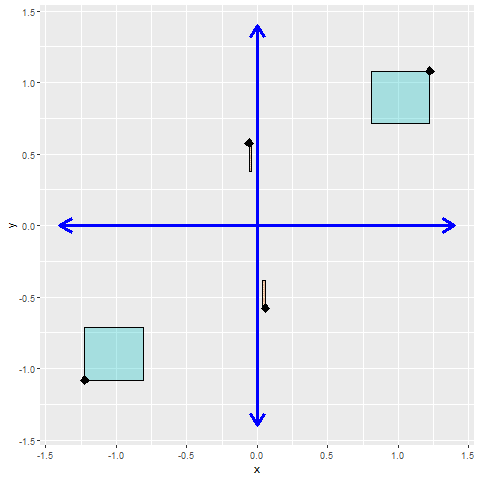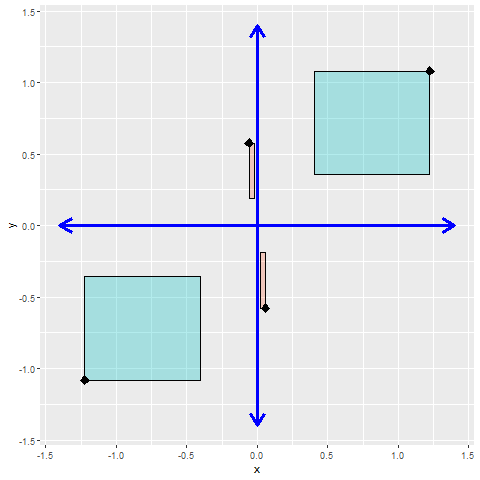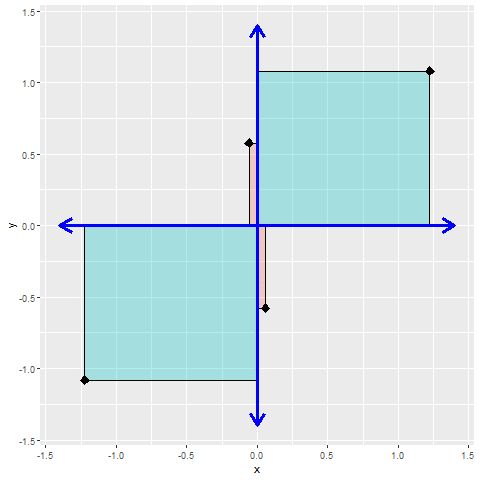
Damit kann man eine symmetrische Matrix aufbauen, in der in der Diagonalen die Varianz = 1 (da wir die Variablen skaliert hatten) und links und rechts der Diagonalen die Kovarianz stehen.
Für mehrere Merkmale kann man eine Matrix der Kovarianzen analog erstellen. Bestimmt man nun aus der Kovarianz-Matrix die Eigenvektoren und ordnet sie in absteigender Reihenfolge ihrer Eigenwerte an, hat man die Hauptkomponenten der Merkmale ermittelt. Der anteilige Beitrag jedes Merkmals in Richtung einer Hauptkomponente entspricht dem Wert der Komponente des Eigenvektors. Er wird auch als Faktorladung bezeichnet. Dieses Verfahren ist als Hauptkomponentenanalyse (Principal Component Analysis, PCA) bekannt.
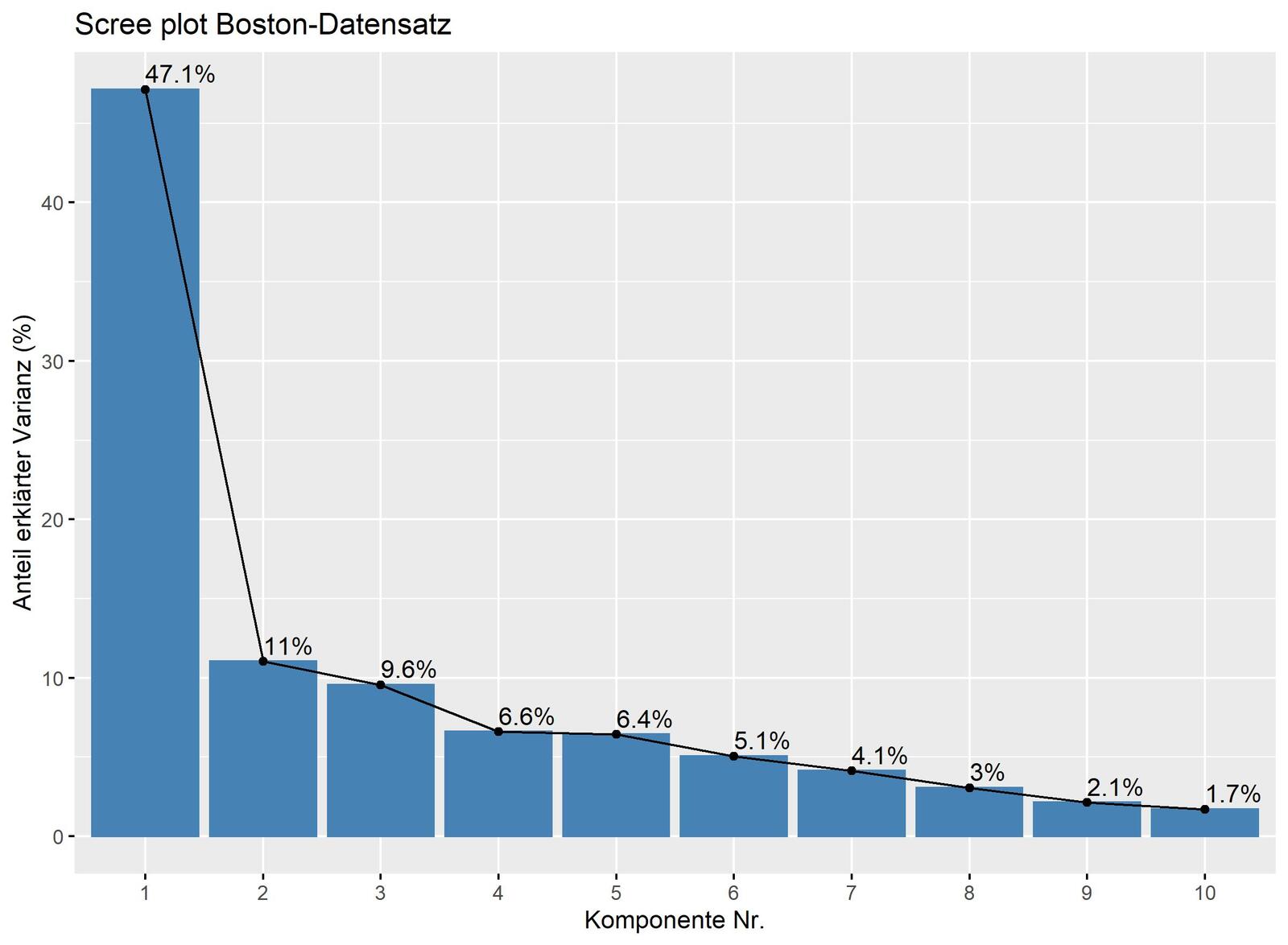
Führt man für die unabhängigen Variablen des Boston-Datensatzes eine Hauptkomponentenanalyse durch, so kann man 68 Prozent der Variation durch lediglich drei Variablen, die ersten drei Hauptkomponenten, ausdrücken (s. Abb. 9).
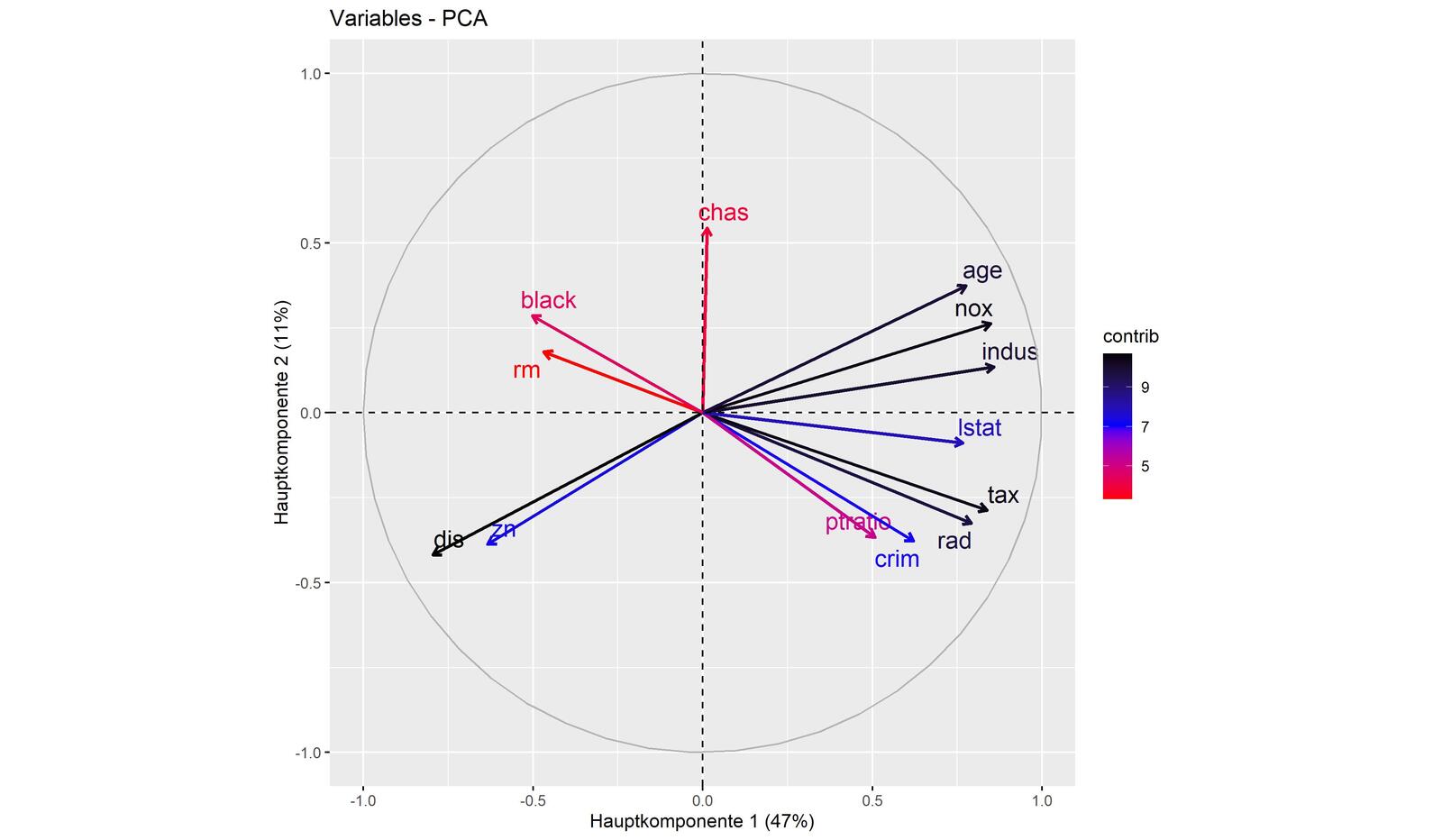
Den Zusammenhang der Merkmale für die beiden ersten Hauptkomponenten zeigt das Ladungsdiagramm (s. Abb. 10). Die Korrelationen der Merkmale sind deutlich zu erkennen.
Führt man jetzt eine lineare Regression mit nur den ersten drei Hauptkomponenten durch, erzielt man damit einen respektablen Wert von R2 = 0,64. Lässt man dagegen alle dreizehn Hauptkomponenten in die Regression mit einfließen, kommt man auf den gleichen Wert von R2 = 0,74 wie im Fall der linearen Regression ohne PCA. Das heißt, man kann Regression mit einer reduzierten Zahl von Variablen betreiben, was natürlich Auswirkungen auf das Bestimmtheitsmaß hat. Da lediglich mit dem Korrelationskoeffizienten gerechnet wird, nutzt die Hauptkomponentenanalyse jedoch lediglich lineare Abhängigkeiten.
Neuronale Netze
Das Perceptron
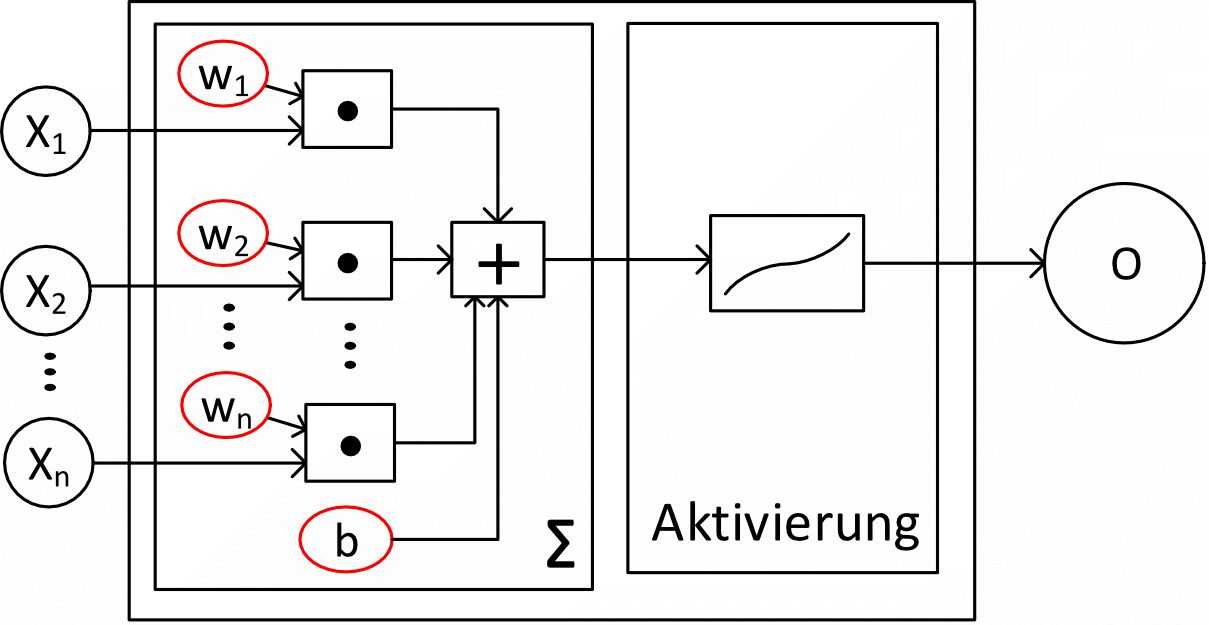
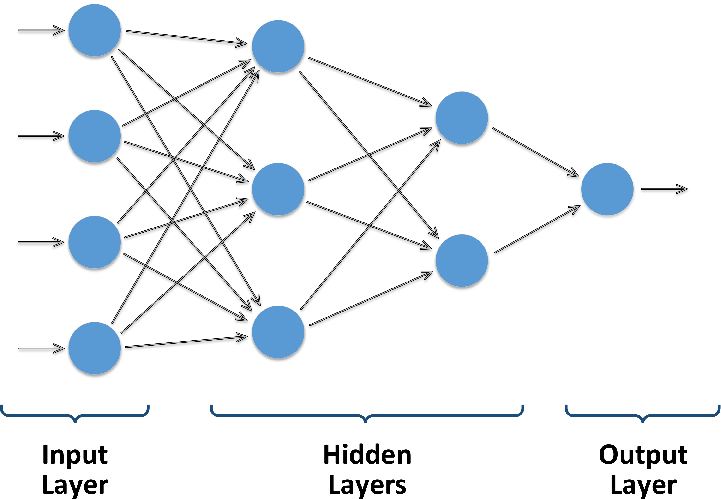
Auch mit neuronalen Netzen lassen sich Regressionen erlernen. Der elementare Grundbaustein neuronaler Netze ist das Perceptron. Sein schematischer Aufbau ist in Abb. 11 gezeigt. Auf der linken Seite (Input) werden Datensätze eingelesen. Durch eine gewichtete Summationsfunktion und eine nachfolgende Aktivierungsfunktion erhält man auf der rechten Seite O (Output) als Ergebnis.
Die Summationsfunktion Σ nimmt die Werte xi von n Eingängen entgegen, multipliziert sie mit den (zu bestimmenden) Gewichtungsfaktoren wi und addiert sie auf. Als Aktivierungsfunktion stehen eine Vielzahl von Funktionstypen zur Verfügung, seien es lineare Funktionen (für Regressionen) oder Sigmoid-Funktionen (für Klassifikationen). Mehrere Perceptrons können nun als Schichten zu einem neuronalen Netz verknüpft werden (Abb. 12). Das Lernen von Netzen mit mehreren Schichten wird als Deep Learning bezeichnet.
Weil jeder Schicht eine eigene Aktivierungsfunktion zugeordnet werden kann, kann durch die Schichtung im Prinzip jede denkbare Funktion nachgebildet werden. Die Gewichte der Perceptrons werden zu den Parametern des Lernvorgangs. Sie werden zu Beginn mit zufälligen Werten belegt. Ausgehend von den Lerndaten und einer vorgegebenen Verlustfunktion werden die Gewichte mit Hilfe des Optimizers so angepasst, dass der Fehler minimal wird.
Damit das Lernen von neuronalen Netzen gelingt, empfiehlt es sich, die Eingangswerte zu normieren. Aber auch dies allein ist noch keine Garantie dafür, dass die Parameter des Netzes erfolgreich erlernt werden. Beispielsweise kann man auch "Netze" mit lediglich einem Perceptron erzeugen. Versucht man damit, die simple Regression in Abb. 7 nachzubilden, kommt man auf keine zufriedenstellenden Ergebnisse [3]. Dies dürfte durch das eingesetzte Verfahren der Gradientenbildung bedingt sein. Je größer die Nichtlinearitäten werden, desto eher können neuronale Netze ihre Stärken ausspielen. Der Boston-Datensatz soll wieder herangezogen werden, um die Lern-Resultate gegenüberzustellen.
Das Framework H2O
Es gibt eine Vielzahl von Werkzeugen, die das maschinelle Lernen unterstützen. Sie setzen ihre Schwerpunkte jedoch meist entweder auf die statistischen Verfahren oder auf neuronale Netze. Im Bereich neuronaler Netze ist Keras/Tensorflow weit verbreitet. Das Werkzeug H2O unterstützt sowohl statistische Verfahren als auch neuronale Netze, ohne dass man die Anwendung wechseln muss [5]. Auch die Kombination von Verfahren mithilfe von AutoML oder Stacked Ensembles ist möglich, welches sich dann aus dem "Besten der Modelle" zusammensetzt.
Bei neuronalen Netzen ist es gängige Praxis, die Daten zufällig in Trainings-, Validierungs- und Testdaten aufzuteilen.
- Die Trainingsdaten werden dazu verwendet, die Parameter anzulernen.
- Die Validierungsdaten dienen dazu, den Lernvorgang zu beobachten und ggf. zu beeinflussen.
- Anhand der Testdaten wird die Leistungsfähigkeit des Lernergebnisses bewertet.
Im vorgestellen Fall wurden zufällig 100 Zeilen als Validierungsdaten herausgegriffen und an 15 verschiedenen Modellen miteinander verglichen. Ein Deep-Learning-Modell mit zwei Layern á 64 Units lieferte die besten Ergebnisse bezogen auf den quadratischen Mittelwert des Fehlers (RMSE), was in etwa einem R2 ≈ 0,92 entspricht. Ein Deep-Learning-Modell mit lediglich einer Unit ist vom Ergebnis her vergleichbar mit einem generalisierten linearen Modell. Bedenkt man, dass medv ≤ 50 beträgt, ist ein Wert von MSE(medv) ≈ 2,59 nicht sonderlich genau.
Tabelle 1: Ergebnisse der verschiedenen Modelle im Vergleich (t: Trainingsdaten; v: Validierungsdaten)
Name | RMSE t | RMSE v | Parameter | ||||
dpl4 gbm2 abst ... dpl2 ... lm1 ... | 1,037 0,053 1,944 ... 4,69 ... 4,61 ... | 2,589 3,087 3,153 ... 4,993 ... 5,027 ... | Deep Learning, 64x64 Units Gradient Boosting, 1000 Bäume automl ... Deep Learning, 1 Unit, mit Regularisierung ... einfaches lineares Modell, Package stats ... | ||||
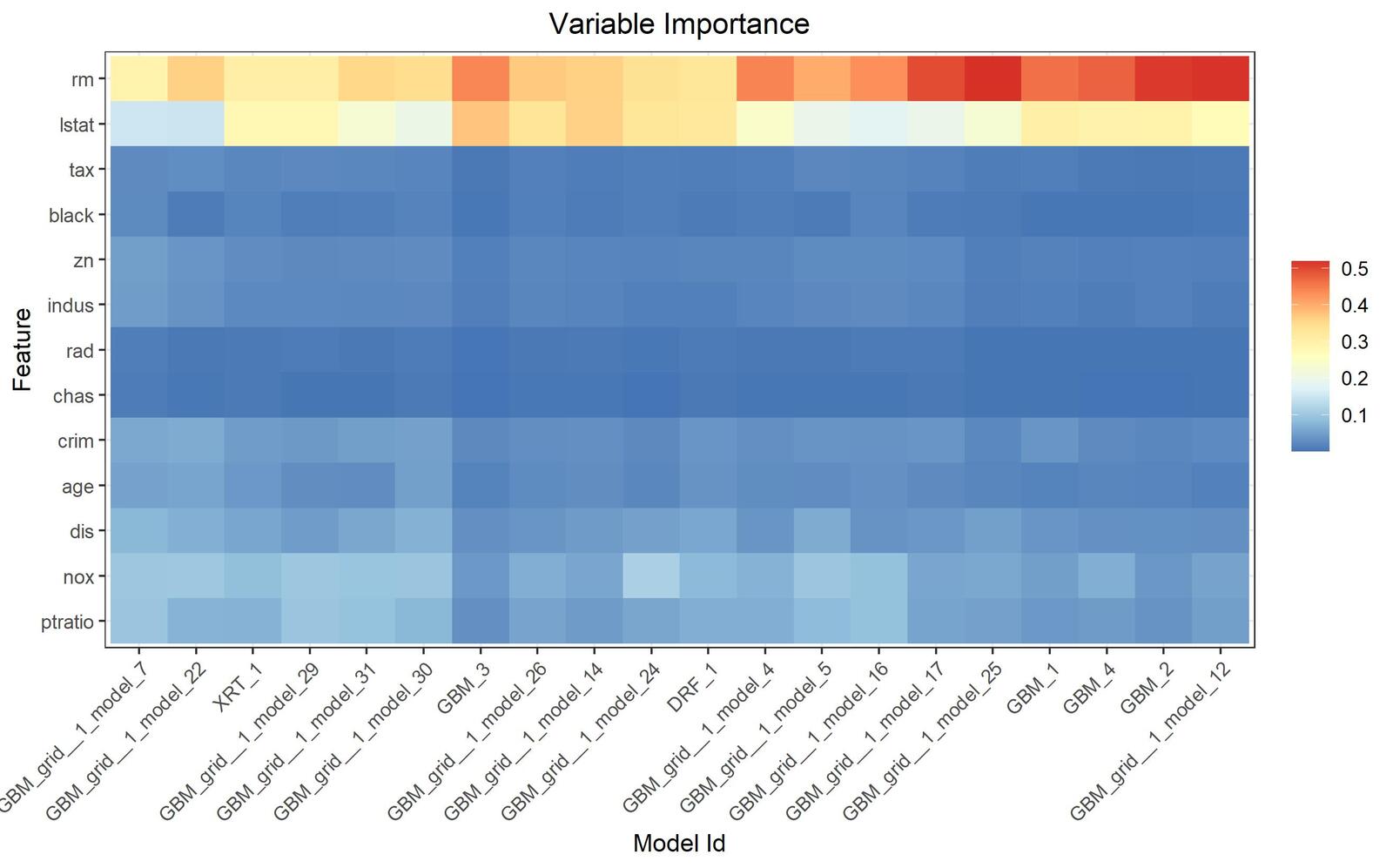
Auch der Einfluss der Variablen im Vergleich der verschiedenen Modelle kann mit H2O dargestellt werden.
Man kann sehen, dass die Anzahl von Räumen (rm) sowie der Status (lstat) den größten Einfluss auf die Hauspreise hat (Abb. 13).
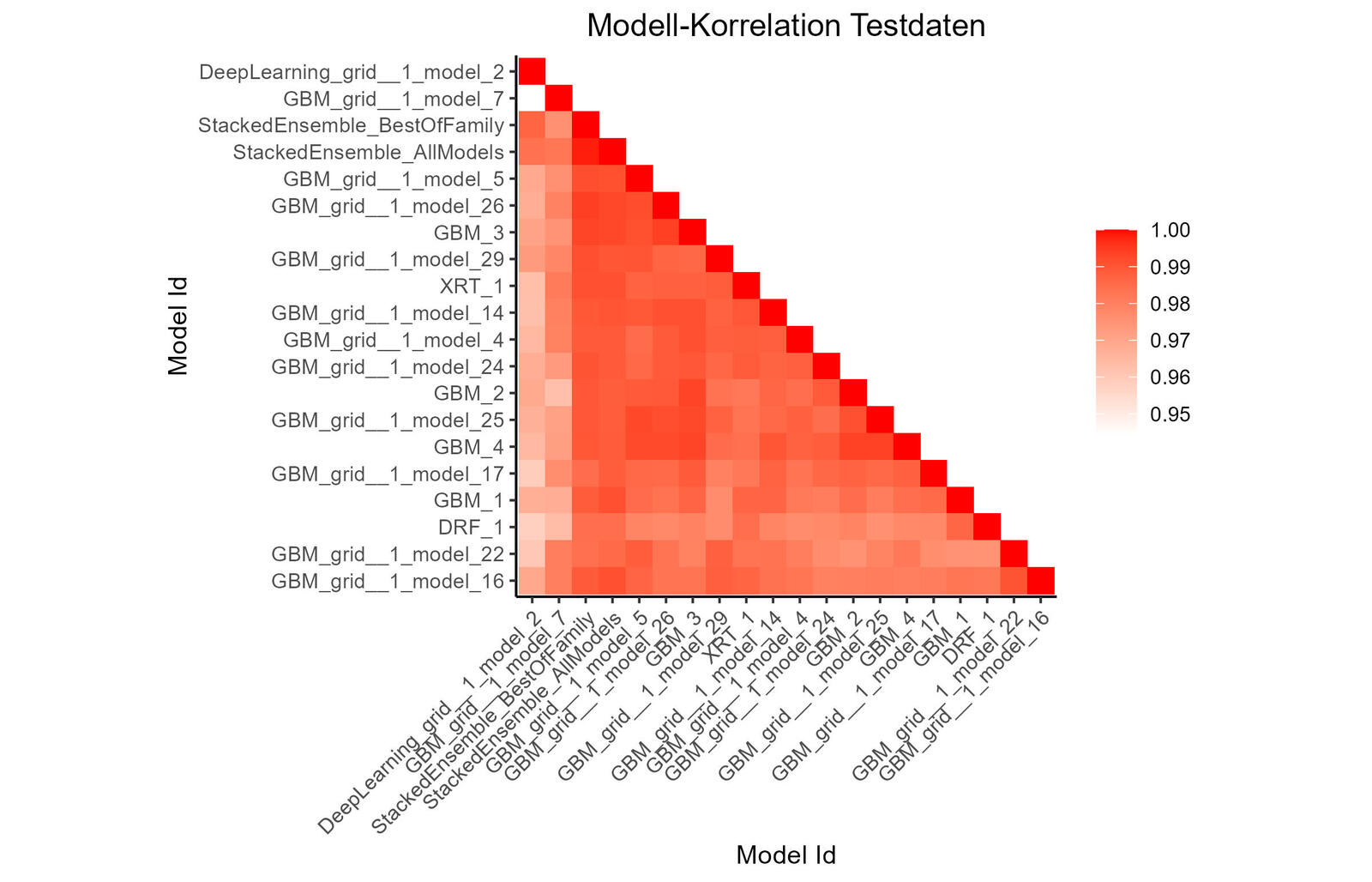
Ein Modell-Korrelations-Diagramm (Abb. 14) zeigt die Korrelation der Vorhersagen der Modelle. Zur Klassifizierung wird die Häufigkeit von Vorhersagen mit minimalen Differenzen verwendet. Standardmäßig werden dann die Modelle nach ihrer Ähnlichkeit (über hierarchisches Clustering) geordnet.
Man sieht, dass das Deep Learning grid 1 model 2 und das GBM grid 1 model 7 kaum mit den anderen Modellen korrelieren. Bei dem Stacked Ensemble sieht es anders aus: Es können wesentlich mehr Gemeinsamkeiten unter den Modellen erkannt werden, was aufgrund der Modelldefinition wenig überrascht. Durch die Analyse-Werkzeuge von H2O kann man somit die Ähnlichkeiten der Modelle bezüglich der Ergebnisse aufspüren und so die Auswahl des eingesetzten Modells untermauern.
Noch eine Bemerkung zu PCA: Wie gezeigt werden konnte, ist der Boston-Datensatz durch neuronale Netze besser zu beschreiben als mit linearen Modellen, da es größere nichtlineare Anteile aufweist. Würde man nun jedoch versuchen, die Variablenzahl durch PCA zu reduzieren, würde dieser Vorteil wieder zunichte gemacht, weil PCA auf dem linearen Modell aufsetzt.
- H. Zou, T. Hastie: Regularization and Variable Selection via the Elastic Net. 2005 (2005)
- Wikipedia: M-Schätzer
- U. Schell: Maschinelles Lernen mit R: Daten aufbereiten und verarbeiten mit H2O und Keras. Carl Hanser Verlag GmbH & Co. KG, 2022
- Delve: The Boston Housing Dataset
- h2o.ai: R Interface for H2O